割り算マスターへの道!子どもが「わかる!」と自信を持つ学習法

「割り算になったら急に分からなくなった…。」といった子どもの声を聞いたことはありませんか?割り算は、足し算・引き算・かけ算とは一味違う複雑さがあるため、苦手に感じる子どもが多い単元です。でも実は、正しい段階を踏めば、子どもは必ず割り算を理解できるようになるんです。
今回は、割り算でつまずく理由や、おすすめの勉強法をご紹介します。日常生活での活用や、今後の学習へのつながりもご紹介しますので、ぜひ参考にしてください。
割り算で子どもがつまずく理由
割り算は、これまでの計算と比べて難易度が上がるため、苦手意識を持つ子どもが多いです。まずは、割り算で子どもがつまずく理由を見ていきましょう。
足す・引く・かけるの全ての要素が含まれている
割り算が難しいと感じる理由の一つは、今まで習った「足す・引く・かける」全ての知識を同時に使わなければならないからです。
例えば、「78÷3」を筆算で解くとき、子どもの頭の中ではこんなことが起こっています。
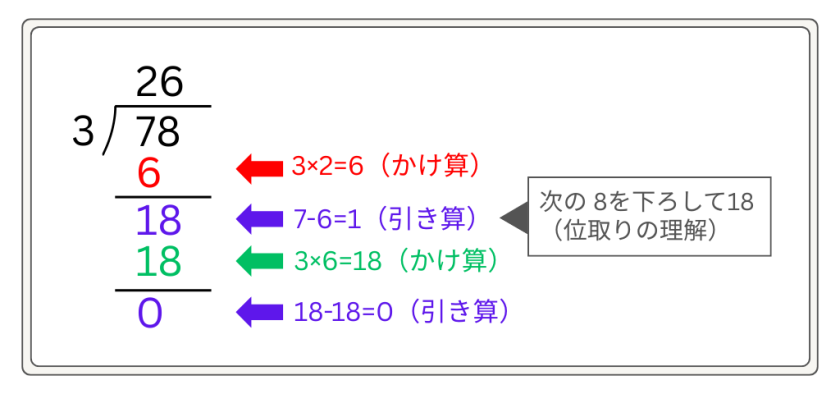
- 「7の中に3はいくつ入るかな?」(かけ算の逆思考)
- 「3×2=6」(かけ算)
- 「7-6=1」(引き算)
- 「次の8を下ろして18にして…」(位取りの理解)
- 「3×6=18」(かけ算)
- 「18-18=0」(引き算)
このように、一つの割り算の中で複数のスキルが必要になります。そのため、九九がまだ完璧でなかったり、繰り下がりの引き算に不安があったりすると、割り算に対する苦手意識が生まれやすくなるんです。
あまりが出る
「12÷3=4」のような割り切れる問題に慣れてきた頃、「あまり」という新しい概念が登場します。あまりが、子どもにとって混乱の元になることが多いです。特に、文章問題になると、同じ計算結果でも問題によって答えが変わる点が難しいところ。以下に例を挙げます。
例1: 「25mのひもを3mずつに切ると何本できる?」 → 25÷3=8あまり1 だから答えは「8本」(残りの1mでは3mのひもは作れないため)
例2: 「25人の子どもが3人乗りのボートに乗ると何艘必要?」 → 25÷3=8あまり1 だから答えは「9艘」(1人残るから追加でもう1艘必要)
同じ「あまり1」でも、状況によって最終的な答えが変わります。そのため、問題文をしっかり読み解いて、あまりの意味を考える読解力と思考力が必要になります。
小数の割り算が難しい
整数の割り算に慣れてきた頃に登場するのが、小数の割り算です。小数自体にまだ戸惑いがある子どもも多く、小数の割り算は急激に難易度が上がったように感じるのです。
小数の割り算では、小数点の位置に注意が必要で、位取りの感覚が求められます。また、商の小数点の位置を正しく決めることが必要であるなど、新しいルールが加わります。このように、整数計算にはない要素が現れるため、子どもがつまずいてしまうのです。
計算方法を段階的に学ぶ
割り算をスムーズに理解するには、段階を踏んで少しずつステップアップすることが大切です。次に、割り算を段階的に学ぶ方法をご紹介します。
繰り下がりのない割り算
割り算学習の最初のステップは、繰り下がりや、あまりのない割り算です。この段階の目的は、子どもに割り算の基本的な概念と、数字を分ける操作の感覚を掴んでもらうことです。
まずは「12÷3=4」や「20÷5=4」のように、九九の範囲で割り切れるシンプルな問題から始めて、割り算の仕組みを掴ませてあげましょう。答えがスッと出る問題を繰り返すことで、できるという実感が生まれ、自信につながります。
また、具体的に分ける体験をさせることが効果的です。例えば、お菓子を12個用意し、3人で同じ数になるように子どもに配らせてみましょう。この体験から、12個を3つに分けると1つのグループに4個入る、という割り算の基本的な意味が理解できます。
あまりのある割り算
繰り下がりのない割り算に慣れてきたら、次はあまりのある割り算です。あまりのある割り算は、最初の大きな壁になることが多いのですが、丁寧に説明し、具体的なイメージを持たせることが乗り越える鍵となります。
あまりとは、割り切れなかった分であることを、繰り返し説明してあげましょう。実際に物を使って試すのも効果的です。例えば、10個のりんごを3人で分ける際には、実際にりんごを3人に3個ずつ配り、最後に1個あまることを目で見て確認してもらいます。その際、あまりは割る数よりも小さくなるという重要なルールもあわせて教えてあげましょう。あまりが割る数と同じか大きくなった場合には、まだ分けられるよ、と計算が間違っていることに気付くよう促してください。
桁の大きい割り算
あまりのある割り算に慣れてきたら、いよいよ桁の大きい割り算、そして筆算へ進みます。筆算は手順が多く複雑に見えますが、一つひとつのステップを丁寧に実行することが重要です。
まずは、1桁で割る割り算からスタートし、徐々に2桁で割る割り算へとステップアップしていきましょう。筆算の際には、「立てる→かける→引く→下ろす」という一連の流れを、声に出して確認しながら練習させると効果的ですよ。
おすすめの勉強法

割り算を得意になるには、計算練習だけでなく、意味を理解しながら学ぶことが重要です。ここでは、家庭でも取り入れやすいおすすめの勉強法を紹介します。
まずは「九九」をマスターする
割り算にはかけ算の知識が不可欠です。まずは九九をマスターしましょう。九九は割り算をスムーズに進めるための基礎です。九九があやふやだと、筆算のスピードが落ちるだけでなく、商を立てるたびに思考が止まってしまい、つまずく原因となってしまいます。
九九をマスターする際には、ただ数字の順番だけでなく、ランダムに質問されても即座に答えられるレベルを目指しましょう。「7×8は?」「4×9は?」といった質問に、間髪入れずに「56」「36」と答えられるように練習します。
練習方法として以下の方法が効果的です。
・声に出してリズムよく唱える
・フラッシュカードを使う
・九九アプリやゲームを活用する
子どもが楽しく続けられる工夫を取り入れてみてください。特に、「36は9×いくつ?」「42は6×いくつ?」などのように、答えからかけ算の式を導き出す逆九九の練習は、割り算の考え方に直結するため積極的に取り入れてください。
文章問題で練習
計算ドリルをこなすだけでは、割り算の本当の意味や実用性を理解することは難しいもの。実用性を理解する際は、「文章問題での練習」が効果的です。文章問題は、割り算がどのような場面で使われるのか、その意味を実感できる練習方法です。
例えば、「6人で24個のお菓子を分けると、1人あたりいくつ?」といった文章問題を解くことで、割り算が分けるという行動と結びついていることを実感できます。問題を読むだけでなく、絵や図を描きながら状況をイメージすると、より理解が深まりますよ。
また、答えだけでなく、なぜその式(24÷6)を立てたのか子ども自身に説明させることも効果的。自分の言葉で説明することで、理解度が格段に深まるのです。
穴あき掛け算で練習
穴あき掛け算は、割り算の逆の考え方を育てるのに効果的な練習法です。割り算が、かけ算の逆の操作であるという関係性を、体感的に理解するのに役立ちます。
例えば、「□×3=15」のような問題では、何をかけたら15になるのか考えることで、割り算の商を求める際の感覚を養えます。また、親子で問題を出し合ったり、時間を計ってスピードを競ったりと、ゲーム感覚で取り組むことで、飽きずに楽しみながら学習できますよ。
筆算であまりの計算を練習
あまりのある計算は、割り切れる問題より複雑になるため、特に丁寧に練習することが大切です。例えば、「7÷3」の場合を見てみましょう。
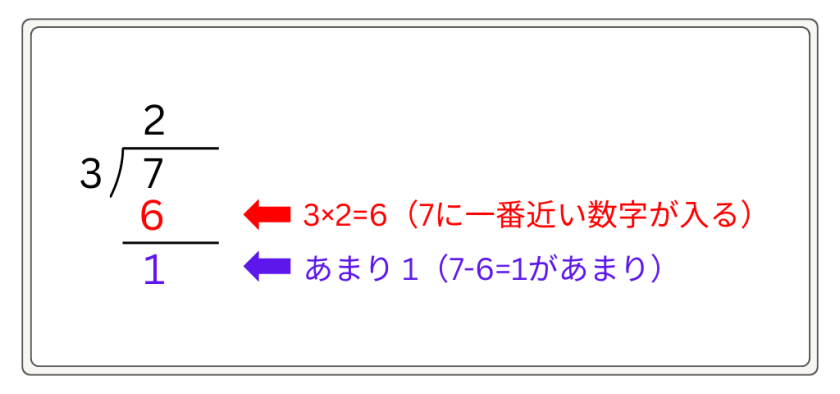
手順としては、「3×2=6で、7に一番近い」→「7-6=1があまり」という流れになります。
あまりのある割り算では、「あまりが割る数より小さいか」を必ず確認させましょう。答えが出たら、「割る数×商+あまり=割られる数」と検算すると効果的です。「3×2+1=7」と確認することにより、答えが正しいか確認できます。検算は、計算力と自信の両方を育ててくれるため、習慣にしましょう。
学習・日常の両方で役立つ割り算

割り算は算数の単元の一つに留まらず、以降の学習や日常生活の様々な場面で活用されています。どんな場面で使われているのかを知ると、学習意欲が高まりますよ。最後に、割り算がどのように役立っているのか、見ていきましょう。
日常生活での活用
割り算は、お金の使い方や人数に応じた配分など、日常生活の様々な場面で活用されています。
例えば、「お小遣いの1,000円を5日間で使うとしたら、1日あたりいくら使えるかな?」のようにお金を計算する場面では、1,000÷5=200円といった割り算の知識が必要です。
また、「クッキーが18枚あるから、3人で同じ数ずつ分けるには?」のように物を均等に配る場面では、18÷3=6枚といった割り算が活用されています。
このように、割り算は日常生活と密接に結びついているのです。
以降の学習の土台となる(分数・小数の土台)
小学校高学年から中学校以降の算数・数学を学ぶ上で、割り算の知識は重要な土台となります。
分数とは、割り算の計算結果を別の形で表現したものとも言えます。例えば、「1÷2」は「0.5」と小数の形で表現されますが、同時に「1/2」(2分の1)という分数で表現されます。また、「3/4」という分数は、「3を4で割る」という意味を内包していますよね。
小数についても同様で、0.1という小数は「1÷10」という割り算で表すことができますし、0.25は「1÷4」と考えることもできます。こうした関係性を理解していると、分数と小数の変換がスムーズになります。
以上のように、割り算は以降の学習の土台となるため、しっかりと理解しておく必要があるでしょう。
まとめ
割り算は、子どもがつまずきやすい単元の一つですが、意味を理解しながら段階的に学ぶことで、少しずつ自信をつけることができます。
お金を何日で使うか、人数で分けるとどうなるかなど、割り算は日常生活で身近に使われています。だからこそ、納得できる体験を積み重ねることが大切です。
今回ご紹介した、おすすめの勉強法を、ぜひご家庭での学習に取り入れてみてください。割り算が得意になると、算数の学習全体に自信がつき、以降の学習においても大きな強みとなりますよ。
関連するコラム
習い事を検索
-
- (428件)
-
-
-
-
-
-









